Soft sheaf

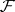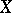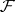A sheaf of sets on a topological space any section of which over some closed subset in can be extended to a section of over all of 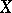. Examples of soft sheaves are: the sheaf of germs of discontinuous sections of an arbitrary sheaf of sets on 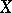; any flabby sheaf 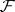on a paracompact space 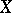; and any fine sheaf 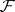of Abelian groups on a paracompact space 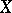. The property of softness of a sheaf 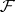on a paracompact space 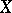is local: A sheaf 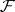is soft if and only if any 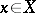has an open neighbourhood 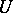such that 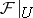is a soft sheaf on 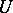. A soft sheaf on a paracompact space induces a soft sheaf on any closed (and, if 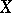is metrizable, any locally closed) subspace. A sheaf of modules over a soft sheaf of rings is a soft sheaf.

If

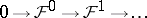is an exact sequence of soft sheaves of Abelian groups on a paracompact space 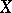, then the corresponding sequence of groups of sections

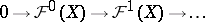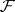is also exact. The cohomology group of any soft sheaf of Abelian groups on a paracompact space 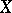is trivial for .

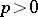References

[1]	R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958)
[2]	R.O. Wells jr., "Differential analysis on complex manifolds" , Springer (1980)

References

[a1]	G.E. Bredon, "Sheaf theory" , McGraw-Hill (1967) pp. §9