Positive-definite function on a group
From Encyclopedia of Mathematics
A continuous function 
on the group 
such that for all 
in 
and 
,
 |
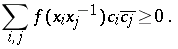Examples can be obtained as follows. Let 
be a unitary representation of 
in a Hilbert space 
, and let 
be a unit (length) vector. Then
 |
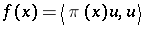is a positive-definite function.
Essentially, these are the only examples. Indeed, there is a bijection between positive-definite functions on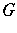 
and isomorphism classes of triples 
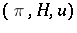consisting of a unitary representation 
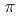of 
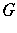on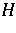 
and a unit vector 
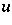that topologically generates 
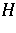under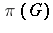 
(a cyclic vector). This is the (generalized) Bochner–Herglotz theorem.
See also Fourier–Stieltjes transform (when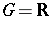 
).
References
| [a1] | S. Lang, "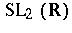 " , Addison-Wesley (1975) pp. Chap. IV, §5 |
| [a2] | G.W. Mackey, "Unitary group representations in physics, probability and number theory" , Benjamin (1978) pp. 147ff |
How to Cite This Entry:
Positive-definite function on a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_function_on_a_group&oldid=43501
Positive-definite function on a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive-definite_function_on_a_group&oldid=43501
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article