Bernoulli integral
of the equations of hydrodynamics
An integral which determines the pressure 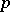 at each point of a stationary flow of an ideal homogeneous fluid or a barotropic gas
at each point of a stationary flow of an ideal homogeneous fluid or a barotropic gas 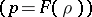 in terms of the velocity
in terms of the velocity  of the flow at that point and the body force function per unit mass
of the flow at that point and the body force function per unit mass 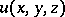 :
:
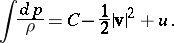 | (1) |
The constant 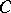 has a specific value for each flow line and varies from one flow line to another. If the motion is potential, the constant
has a specific value for each flow line and varies from one flow line to another. If the motion is potential, the constant 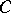 is the same for the entire flow.
is the same for the entire flow.
For a non-stationary flow, the Bernoulli integral (sometimes called the Cauchy–Lagrange integral) holds in the presence of a velocity potential:
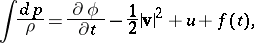 | (2) |
where
 |
and  is an arbitrary function of time.
is an arbitrary function of time.
For an incompressible liquid the left-hand sides of equations (1) and (2) are converted to the 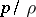 form; for a barotropic gas
form; for a barotropic gas 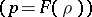 to the form
to the form
 |
The integral was presented by D. Bernoulli in 1738.
References
| [1] | L.M. Milne-Thomson, "Theoretical hydrodynamics" , Macmillan (1950) |
Bernoulli integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_integral&oldid=43482