Chebyshev equation
The linear homogeneous second-order ordinary differential equation
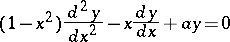 |
or, in self-adjoint form,
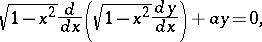 |
where  is a constant. Chebyshev's equation is a special case of the hypergeometric equation.
is a constant. Chebyshev's equation is a special case of the hypergeometric equation.
The points 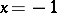 and
and 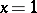 are regular singular points (cf. Regular singular point) of the Chebyshev equation. Substituting the independent variable
are regular singular points (cf. Regular singular point) of the Chebyshev equation. Substituting the independent variable
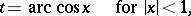 |
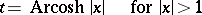 |
reduces this equation to a corresponding linear equation with constant coefficients:
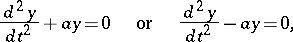 |
so that Chebyshev's equation can be integrated in closed form. A fundamental systems of solutions to Chebyshev's equation on the interval 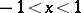 with
with  , where
, where  is a natural number, consists of the Chebyshev polynomials (of the first kind) of degree
is a natural number, consists of the Chebyshev polynomials (of the first kind) of degree  ,
,
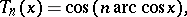 |
and the functions 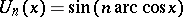 , which are related to Chebyshev polynomials of the second kind. The polynomial
, which are related to Chebyshev polynomials of the second kind. The polynomial 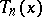 is a real solution to Chebyshev's equation on the entire real line, with
is a real solution to Chebyshev's equation on the entire real line, with  . Chebyshev's equation is also studied in complex domains.
. Chebyshev's equation is also studied in complex domains.
Chebyshev equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_equation&oldid=43461