Equiconvergent series

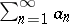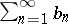Convergent or divergent series and whose difference is a convergent series with zero sum: 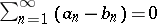. If their difference is only a convergent series, then the series are called equiconvergent in the wide sense.

If 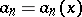and 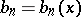are functions, for example, 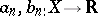, where 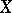is any set and 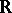is the set of real numbers, then the series 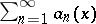and 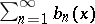are called uniformly equiconvergent (uniformly equiconvergent in the wide sense) on 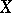if their difference is a series that is uniformly convergent on 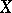with sum zero (respectively, only uniformly convergent on ).

Example. If two integrable functions on 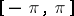are equal on an interval 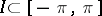, then their Fourier series are uniformly equiconvergent on every interval 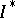interior to 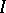, and the conjugate Fourier series are uniformly equiconvergent in the wide sense on .