Local decomposition

local cut

A closed set 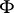in the space is a local cut if there are a point (a point at which the set 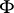cuts the space) and a positive number such that for any number 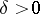there is in the open set 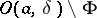, where 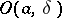is the (open) ball of radius 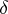with centre at , a pair of points with the following property: Any continuum lying in 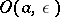and containing this pair of points has a non-empty intersection with 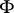. K. Menger and P.S. Urysohn proved that a closed set 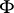lying in a plane has dimension 1 if and only if it does not contain interior (with respect to the plane) points and locally cuts the plane (at one point at least).

A similar characterization of closed 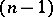-dimensional sets in the -dimensional space 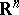was given by P.S. Aleksandrov (see Local linking).