Local linking
A property of the disposition of a closed set 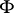 close to a point
close to a point  of it in a Euclidean space
of it in a Euclidean space 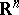 . It consists of the existence of a number
. It consists of the existence of a number 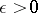 such that, for any positive number
such that, for any positive number 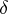 , in the open set
, in the open set 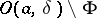 there lies a
there lies a 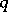 -dimensional cycle
-dimensional cycle 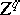 ,
, 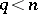 , with integer coefficients, having the following property: Any compact set
, with integer coefficients, having the following property: Any compact set 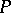 lying in
lying in 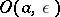 in which
in which 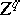 is homologous to zero has non-empty intersection with
is homologous to zero has non-empty intersection with 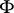 . Here
. Here 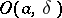 and
and 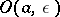 are spheres with centre
are spheres with centre  and radii
and radii 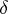 and
and  . Without changing the content of this definition one can restrict oneself to compact sets
. Without changing the content of this definition one can restrict oneself to compact sets 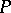 that are polyhedra. For
that are polyhedra. For 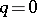 the concept of a local linking goes over to the concept of a local cut (cf. Local decomposition). Aleksandrov's obstruction theorem: In order that
the concept of a local linking goes over to the concept of a local cut (cf. Local decomposition). Aleksandrov's obstruction theorem: In order that  it is necessary and sufficient that the number
it is necessary and sufficient that the number 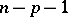 should be the smallest integer
should be the smallest integer 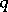 for which there is a
for which there is a 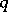 -dimensional linking of
-dimensional linking of  in
in 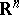 close to some point
close to some point 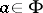 . An analogous theorem has been proved concerning obstructions "modulo m" , which characterizes sets
. An analogous theorem has been proved concerning obstructions "modulo m" , which characterizes sets 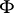 that have homological dimension
that have homological dimension  "modulo m" .
"modulo m" .
Far-reaching generalizations of obstruction theorems are theorems on the homological containment of compact sets.
References
| [1] | P.S. Aleksandrov, "An introduction to homological dimension theory and general combinatorial topology" , Moscow (1975) (In Russian) |
| [2] | K. Sitnikov, "On homological girdling of compacta in Euclidean space" Dokl. Akad. Nauk SSSR , 81 (1951) pp. 153–156 (In Russian) |
Local linking. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_linking&oldid=43441