Minimax estimator

A statistical estimator obtained as a result of the application of the notion of a minimax statistical procedure in the problem of statistical estimation.

Example 1. Let a random variable be subject to the binomial law with parameters and 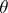, where , , is unknown. The statistic

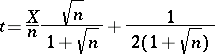is a minimax estimator for the parameter 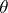with respect to the loss function

Example 2. Let be independent random variables subject to the same probability law, with a continuous probability density 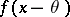, , 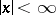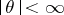. The Pitman estimator

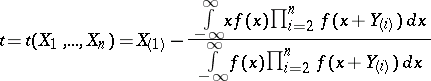is a minimax estimator for the unknown shift parameter 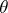relative to the loss function 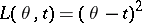, where 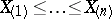are the order statistics (cf. Order statistic) obtained from the sample 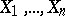and 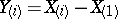. In particular, if , then .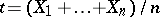

References

[1]	S. Zacks, "The theory of statistical inference" , Wiley (1971)
[2]	D.R. Cox, D.V. Hinkley, "Theoretical statistics" , Chapman & Hall (1974)