Projective normal

A generalization of the concept of a normal in metric geometry. Distinct from the latter, where a normal is totally determined by the tangent plane to a surface (i.e. the first-order neighbourhood), this does not hold in projective geometry. Even terms of the first order of smallness do not determine the vertices of a coordinate tetrahedron not lying in the tangent plane (i.e. for a chosen Darboux quadric it is impossible to construct a single self-polar tetrahedron). This is a natural situation: the projective group is much larger than the group of motions, and therefore its invariants must be of higher order; but even in the fourth-order neighbourhood there is no unique straight line that could be taken as the third axis of a tetrahedron. In this way one obtains, e.g.:

the Wilczynski directrix

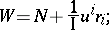the Green edge

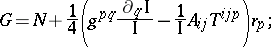the Čech axis

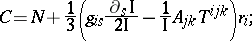and the Fubini normal

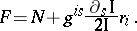Here 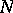is the affine normal.

They all lie in one plane.

References

[1]	P.A. Shirokov, A.P. Shirokov, "Differentialgeometrie" , Teubner (1962) (Translated from Russian)
[2]	A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian)
[3]	S.P. Finikov, "Projective differential geometry" , Moscow-Leningrad (1937) (In Russian)

References

[a1]	G. Bol, "Projektive differentialgeometrie" , I, II , Vandenhoeck & Ruprecht (1950)
[a2]	E. Cartan, "Leçons sur la théorie des espaces à connexion projective" , Gauthier-Villars (1937)
[a3]	G. Fubini, E. Čech, "Introduction á la géométrie projective différentielle des surfaces" , Gauthier-Villars (1931)