De Rham cohomology
of an algebraic variety
A cohomology theory of algebraic varieties based on differential forms. To every algebraic variety 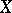 over a field
over a field 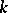 is associated a complex of regular differential forms (see Differential form on an algebraic variety); its cohomology groups
is associated a complex of regular differential forms (see Differential form on an algebraic variety); its cohomology groups 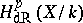 are called the de Rham cohomology groups of
are called the de Rham cohomology groups of 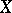 . If
. If 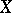 is a smooth complete variety and if
is a smooth complete variety and if 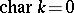 , then de Rham cohomology is a special case of Weil cohomology (see [2], [3]). If
, then de Rham cohomology is a special case of Weil cohomology (see [2], [3]). If 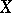 is a smooth affine variety and if
is a smooth affine variety and if 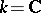 , then the following analogue of the de Rham theorem is valid:
, then the following analogue of the de Rham theorem is valid:
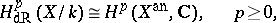 |
where 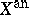 is the complex-analytic manifold corresponding to the algebraic variety
is the complex-analytic manifold corresponding to the algebraic variety 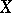 (see [1]). For example, if
(see [1]). For example, if 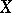 is the complement of an algebraic hypersurface in
is the complement of an algebraic hypersurface in 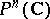 , then the cohomology group
, then the cohomology group 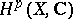 can be calculated using rational differential forms on
can be calculated using rational differential forms on 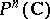 with poles on this hypersurface.
with poles on this hypersurface.
For any morphism 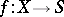 it is possible to define the relative de Rham complex
it is possible to define the relative de Rham complex 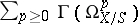 (see Derivations, module of), which results in the relative de Rham cohomology groups
(see Derivations, module of), which results in the relative de Rham cohomology groups 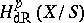 . If
. If 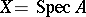 and
and 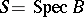 are affine, the relative de Rham complex coincides with
are affine, the relative de Rham complex coincides with 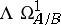 . The cohomology groups
. The cohomology groups 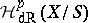 of the sheaf complex
of the sheaf complex 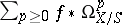 on
on 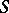 are called the relative de Rham cohomology sheaves. These sheaves are coherent on
are called the relative de Rham cohomology sheaves. These sheaves are coherent on 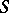 if
if 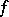 is a proper morphism.
is a proper morphism.
References
| [1] | A. Grothendieck, "On the de Rham cohomology of algebraic varieties" Publ. Math. IHES , 29 (1966) pp. 351–359 |
| [2] | R. Hartshorne, "Ample subvarieties of algebraic varieties" , Springer (1970) |
| [3] | R. Hartshorne, "On the de Rham cohomology of algebraic varieties" Publ. Math. IHES , 45 (1975) pp. 5–99 |
De Rham cohomology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_Rham_cohomology&oldid=43366