Lehmer conjecture
A conjecture about the minimal Mahler measure of a non-zero algebraic integer which is not a root of unity. The Mahler measure 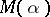 of an algebraic number
of an algebraic number 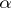 is defined by
is defined by
 | (a1) |
where 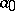 denotes the leading coefficient and
denotes the leading coefficient and 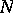 is the degree of the minimal polynomial
is the degree of the minimal polynomial 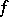 (with integral coefficients) of
(with integral coefficients) of 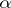 (cf. also Algebraic number) and
(cf. also Algebraic number) and 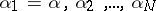 are its conjugates. Since
are its conjugates. Since  depends only on
depends only on 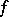 , it is also denoted by
, it is also denoted by 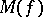 and called the Mahler measure of
and called the Mahler measure of 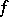 . Jensen's formula (cf. also Jensen formula) implies the equality
. Jensen's formula (cf. also Jensen formula) implies the equality
 |
and this observation permits one to generalize Mahler's measure to polynomials in several variables (see [a11], [a13]).
A theorem of L. Kronecker implies that if 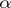 is an algebraic integer with
is an algebraic integer with 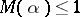 , then
, then 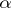 is either zero or a root of unity. D.H. Lehmer [a7] asked whether
is either zero or a root of unity. D.H. Lehmer [a7] asked whether 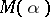 could attain values arbitrarily close to
could attain values arbitrarily close to 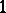 . This subsequently led to the following formulation of Lehmer's conjecture: There exists a positive constant
. This subsequently led to the following formulation of Lehmer's conjecture: There exists a positive constant 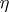 such that if
such that if 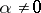 is an algebraic integer, not a root of unity, then
is an algebraic integer, not a root of unity, then
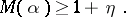 |
Lehmer's conjecture is equivalent to the existence of ergodic automorphisms of the infinite-dimensional torus having finite entropy [a8] and its truth would imply the following conjecture stated by A. Schinzel and H. Zassenhaus [a16]: There exists a positive constant 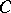 with the property that if
with the property that if 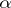 is a non-zero algebraic integer of degree
is a non-zero algebraic integer of degree  , not a root of unity, then
, not a root of unity, then 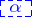 , the maximal absolute value of a conjugate of
, the maximal absolute value of a conjugate of 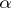 is at least
is at least
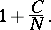 |
It is known ([a2], [a14]) that Lehmer's conjecture holds for non-reciprocal integers 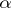 , i.e. algebraic integers whose minimal polynomials do not have
, i.e. algebraic integers whose minimal polynomials do not have 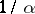 as a root. In this case the minimal value for
as a root. In this case the minimal value for 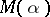 equals
equals 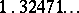 and is attained by roots of the polynomial
and is attained by roots of the polynomial 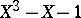 .
.
In 1971, P.E. Blanksby and H.L. Montgomery [a1] established, for all algebraic integers 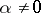 of degree
of degree 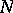 that are not roots of unity, the inequality
that are not roots of unity, the inequality
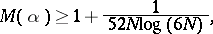 |
and subsequently E. Dobrowolski [a4] obtained
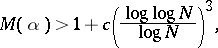 |
with 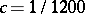 , whereas for
, whereas for 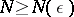 he got
he got  . Subsequently, several authors increased the value of
. Subsequently, several authors increased the value of  to
to 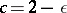 ([a3], [a12]) and
([a3], [a12]) and  ([a9]). Since for non-reciprocal integers
([a9]). Since for non-reciprocal integers 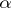 one has
one has  , the last result leads to the inequality
, the last result leads to the inequality
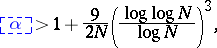 |
but this has been superseded by A. Dubickas [a5], who proved for sufficiently large  the inequality
the inequality
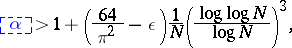 |
which is the strongest known result toward the Schinzel–Zassenhaus conjecture as of 2000.
The smallest known value of 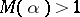 is
is  , realized by the root of
, realized by the root of 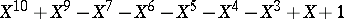 and found in [a7].
and found in [a7].
References
| [a1] | P.E. Blanksby, H.L. Montgomery, "Algebraic integers near the unit circle" Acta Arith. , 18 (1971) pp. 355–369 |
| [a2] | K. Breusch, "On the distribution of the roots of a polynomial with integral coefficients" Proc. Amer. Math. Soc. , 3 (1951) pp. 939–941 |
| [a3] | D.G. Cantor, E.G. Straus, "On a conjecture of D.H. Lehmer" Acta Arith. , 42 (1982) pp. 97–100; 325 |
| [a4] | E. Dobrowolski, "On a question of Lehmer and the number of irreducible factors of a polynomial" Acta Arith. , 34 (1979) pp. 391–401 |
| [a5] | A. Dubickas, "On algebraic numbers of small measure" Liet. Mat. Rink. , 35 (1995) pp. 421–431 |
| [a6] | A. Dubickas, "Algebraic conjugates outside the unit circle" , New Trends in Probability and Statistics , 4 (1997) pp. 11–21 |
| [a7] | D.H. Lehmer, "Factorization of certain cyclotomic functions" Ann. Math. , 34 : 2 (1933) pp. 461–479 |
| [a8] | D.A. Lind, K. Schmidt, T. Ward, "Mahler measure and entropy for commuting automorphisms of compact groups" Invent. Math. , 101 (1990) pp. 503–629 |
| [a9] | R. Louboutin, "Sur la mesure de Mahler d'un nombre algébrique" C.R. Acad. Sci. Paris , 296 (1983) pp. 707–708 |
| [a10] | K. Mahler, "An application of Jensen's formula to polynomials" Mathematika , 7 (1960) pp. 98–100 |
| [a11] | K. Mahler, "On some inequalities for polynomials in several variables" J. London Math. Soc. , 37 (1962) pp. 341–344 |
| [a12] | U. Rausch, "On a theorem of Dobrowolski about the product of conjugate numbers" Colloq. Math. , 50 (1985) pp. 137–142 |
| [a13] | A. Schinzel, "The Mahler measure of polynomials" , Number Theory and its Applications (Ankara, 1996) , M. Dekker (1999) pp. 171–183 |
| [a14] | C.J. Smyth, "On the product of the conjugates outside the unit circle of an algebraic integer" Bull. London Math. Soc. , 3 (1971) pp. 169–175 |
| [a15] | C.L. Stewart, "Algebraic integers whose conjugates lie near the unit circle" Bull. Soc. Math. France , 196 (1978) pp. 169–176 |
| [a16] | A. Schinzel, H. Zassenhaus, "A refinement of two theorems of Kronecker" Michigan J. Math. , 12 (1965) pp. 81–85 |
Lehmer conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lehmer_conjecture&oldid=43023