Distribution modulo one, higher-dimensional
The distribution of the fractional parts 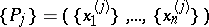 of a sequence
of a sequence 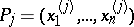 of elements of the
of elements of the  -dimensional Euclidean space in the
-dimensional Euclidean space in the  -dimensional unit cube
-dimensional unit cube 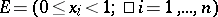 . Here
. Here  denotes the fractional part of a number.
denotes the fractional part of a number.
The sequence 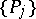 ,
, 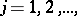 is said to be uniformly distributed in
is said to be uniformly distributed in 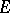 if the equality
if the equality
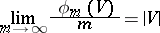 |
holds for any rectangle 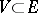 , where
, where 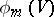 is the number of those points among the first
is the number of those points among the first  members of the sequence which belong to
members of the sequence which belong to 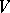 and
and 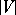 is the measure of
is the measure of 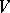 .
.
A sequence 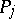 ,
, 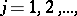 is said to be uniformly distributed modulo one if the corresponding sequence of fractional parts
is said to be uniformly distributed modulo one if the corresponding sequence of fractional parts 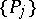 is uniformly distributed in
is uniformly distributed in 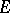 .
.
Weyl's criterion for higher-dimensional distribution modulo one.
A sequence 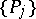 ,
, 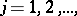 is uniformly distributed in
is uniformly distributed in 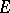 if and only if
if and only if
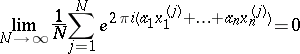 |
for any set of integers 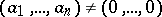 . A particular case of this theorem is the Weyl criterion for a sequence of real numbers to be uniformly distributed modulo one. Weyl's criterion implies the following theorem of Kronecker: Let
. A particular case of this theorem is the Weyl criterion for a sequence of real numbers to be uniformly distributed modulo one. Weyl's criterion implies the following theorem of Kronecker: Let 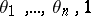 be real numbers that are linearly independent over the field of rational numbers, let
be real numbers that are linearly independent over the field of rational numbers, let  be arbitrary real numbers and let
be arbitrary real numbers and let 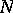 and
and  be positive numbers; then there are integers
be positive numbers; then there are integers 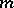 and
and  such that
such that
 |
for all 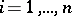 . In other words, the sequence
. In other words, the sequence 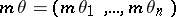 ,
, 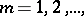 is uniformly distributed modulo one.
is uniformly distributed modulo one.
References
| [1] | J.W.S. Cassels, "An introduction to diophantine approximation" , Cambridge Univ. Press (1957) |
Comments
For additional references see Distribution modulo one.
Distribution modulo one, higher-dimensional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distribution_modulo_one,_higher-dimensional&oldid=42944