Well-posed problem
The problem of determining a solution 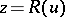 in a metric space
in a metric space 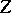 (with distance
(with distance 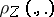 ) from initial data
) from initial data  in a metric space
in a metric space 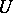 (with distance
(with distance 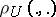 ), satisfying the following conditions: a) for any
), satisfying the following conditions: a) for any 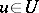 there exists a solution
there exists a solution 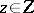 ; b) the solution is uniquely defined; c) the problem is stable with respect to the spaces
; b) the solution is uniquely defined; c) the problem is stable with respect to the spaces 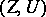 : For any
: For any 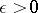 there exists a
there exists a 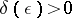 such that, for any
such that, for any 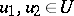 , the inequality
, the inequality 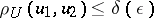 implies
implies 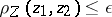 , where
, where 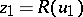 ,
, 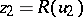 .
.
Problems not satisfying one of these conditions for well-posedness are called ill-posed problems.
Comments
The term "well-posed" (also properly posed or correctly set) was coined by the French mathematician J. Hadamard at the beginning of the 19th century [a1]. In particular, he stressed the importance of continuous dependence of solutions on the data (i.e. property 3). Practical problems (e.g. in hydrodynamics, seismology) lead not seldom to formulations that are ill-posed (cf. Ill-posed problems).
References
| [a1] | J. Hadamard, "Lectures on Cauchy's problem in linear partial differential equations" , Dover, reprint (1952) (Translated from French) |
| [a2] | P.R. Garabedian, "Partial differential equations" , Wiley (1964) |
Well-posed problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Well-posed_problem&oldid=42887