Chebyshev centre
of a bounded set 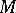 in a metric space
in a metric space 
An element 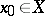 for which
for which
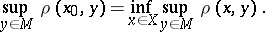 | (*) |
The quantity (*) is the Chebyshev radius of the set 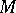 . If a normed linear space is dual to some normed linear space, then any bounded set
. If a normed linear space is dual to some normed linear space, then any bounded set 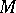 has at least one Chebyshev centre. There exists a Banach space and a three-point set in it that has no Chebyshev centre. Every bounded set in a Banach space
has at least one Chebyshev centre. There exists a Banach space and a three-point set in it that has no Chebyshev centre. Every bounded set in a Banach space 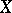 has at most one Chebyshev centre if and only if
has at most one Chebyshev centre if and only if 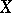 is uniformly convex in every direction, that is, if for any
is uniformly convex in every direction, that is, if for any 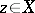 and any
and any 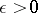 there exists a number
there exists a number 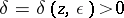 such that if
such that if 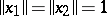 ,
, 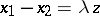 and
and  , then
, then  . The Chebyshev centre of every bounded set
. The Chebyshev centre of every bounded set 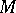 in a normed linear space
in a normed linear space  of dimension greater than two is contained in the convex hull of that set if and only if
of dimension greater than two is contained in the convex hull of that set if and only if  is a Hilbert space. A Chebyshev centre is a special case of the more general notion of a best
is a Hilbert space. A Chebyshev centre is a special case of the more general notion of a best  -lattice.
-lattice.
References
| [1] | Itogi Nauki. Mat. Anal. 1967 (1969) pp. 75–132 |
Chebyshev centre. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebyshev_centre&oldid=42865