Cotes formulas

Formulas for the approximate computation of definite integrals, given the values of the integrand at finitely many equidistant points, i.e. quadrature formulas with equidistant interpolation points (cf. Quadrature formula). Cotes' formulas are

(*)

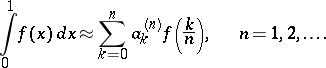The numbers 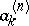are known as Cotes' coefficients; they are determined from the condition that formula (*) be exact if 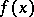is a polynomial of degree at most .

The formulas were proposed by R. Cotes (1722) and considered in a more general form by I. Newton. See Newton–Cotes quadrature formula.

Comments

Cotes' formulas were published in [a2] after Cotes' death. In the Western literature these formulas are known as the Newton–Cotes formulas. A detailed analysis of them can be found in [a1], [a3], [a4].

References

[a1]	H. Brass, "Quadraturverfahren" , Vandenhoeck & Ruprecht (1977)
[a2]	R. Cotes, "Harmonia Mensurarum" , 1–2 , London (1722) (Published by R. Smith after Cotes' death)
[a3]	P.J. Davis, P. Rabinowitz, "Methods of numerical integration" , Acad. Press (1984)
[a4]	H. Engels, "Numerical quadrature and cubature" , Acad. Press (1980)