Bicyclic semi-group
The semi-group with unit element and two generators 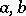 subject to the single generating relation
subject to the single generating relation 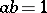 . One of the realizations of the bicyclic semi-group is the Cartesian square
. One of the realizations of the bicyclic semi-group is the Cartesian square 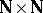 , where
, where 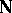 is the set of non-negative integers, with respect to the operation
is the set of non-negative integers, with respect to the operation
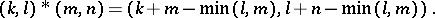 |
The bicyclic semi-group is an inversion semi-group and as such is monogenic, i.e. is generated by a single element. The idempotents (cf. Idempotent) of the bicyclic semi-group form a chain, which is ordered with respect to the type of the positive numbers. The bicyclic semi-group is bisimple (cf. Simple semi-group).
The bicyclic semi-group often occurs in theoretical investigations concerning semi-groups, not only as a representative of certain important classes of semi-groups, but also as a "block" , which defines the structure of individual semi-groups. Thus, for any idempotent  of a
of a  -simple, but not completely
-simple, but not completely  -simple semi-group
-simple semi-group 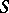 there exists a bicyclic sub-semi-group in
there exists a bicyclic sub-semi-group in  containing
containing  as the unit element (cf. [1], Para. 2.7). The elements
as the unit element (cf. [1], Para. 2.7). The elements  and
and 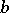 of the bicyclic semi-group
of the bicyclic semi-group  defined as above, are, respectively, its left and right multiplying elements (i.e. there exist proper subsets
defined as above, are, respectively, its left and right multiplying elements (i.e. there exist proper subsets 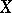 and
and 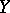 in
in  such that
such that  ,
, 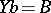 ). Moreover, in a semi-group
). Moreover, in a semi-group 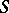 with unit element
with unit element  the element
the element  will be a left multiplier if and only if
will be a left multiplier if and only if 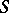 contains the bicyclic semi-group whose unit element is identical with
contains the bicyclic semi-group whose unit element is identical with  ; a similar theorem is also valid for right multiplying elements, so that
; a similar theorem is also valid for right multiplying elements, so that 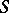 has left multiplying elements if and only if it also has right multiplying elements.
has left multiplying elements if and only if it also has right multiplying elements.
References
| [1] | A.H. Clifford, G.B. Preston, "Algebraic theory of semi-groups" , 1–2 , Amer. Math. Soc. (1961–1967) |
| [2] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
Bicyclic semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bicyclic_semi-group&oldid=42741