Distributions, complete family of

A family of probability measures 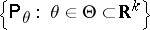, defined on a measure space 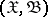, for which the unique unbiased estimator of zero in the class of 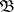-measurable functions on 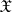is the function identically equal to zero, that is, if 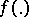is any 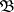-measurable function defined on 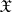satisfying the relation

(*)

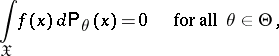then 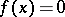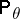-almost-everywhere, for all 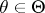. For example, a family of exponential distributions is complete. If the relation (*) is satisfied under the further assumption that 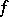is bounded, then the family 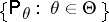is said to be boundedly complete. Boundedly-complete families of distributions of sufficient statistics play a major role in mathematical statistics, in particular in the problem of constructing similar tests (cf. Similar test) with a Neyman structure.

References

[1]	Yu.V. Linnik, "Statistical problems with nuisance parameters" , Amer. Math. Soc. (1968) (Translated from Russian)
[2]	E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959)

References

[a1]	S. Zacks, "The theory of statistical inference" , Wiley (1971)