Saccheri quadrangle

A quadrangle 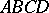, right-angled at 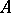and 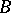and with equal sides 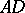and 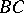. It was discussed by G. Saccheri (1733) in attempts to prove Euclid's fifth postulate about parallel lines. Of the three possibilities regarding the angles at 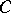and 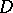: they are right angles, they are obtuse angles or they are acute angles, the first is equivalent to Euclid's fifth postulate, and the second leads to spherical or elliptic geometry. As regards the third possibility, Saccheri made the erroneous deduction that it also contradicts the other axioms and postulates of Euclid.

References

[1]	V.F. Kagan, "Foundations of geometry" , 1 , Moscow-Leningrad (1949) (In Russian)
[2]	A.V. Pogorelov, "Foundations of geometry" , Noordhoff (1966) (Translated from Russian)

References

[a1]	R. Bonola, "Non-Euclidean geometry" , Dover, reprint (1955) pp. 23 (Translated from Italian)
[a2]	H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 5, 190
[a3]	N.V. Efimov, "Higher geometry" , MIR (1980) (Translated from Russian)
[a4]	K. Borsuk, W. Szmielew, "Foundations of geometry" , North-Holland (1960)