Zassenhaus group

A doubly-transitive group 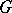of permutations on a finite set 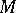(cf. Permutation group) in which only the identity permutation fixes more than two elements of 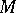and such that for any pair 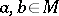the subgroup 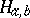is non-trivial, where

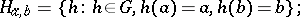such groups were first considered by H. Zassenhaus in [1]. The class of Zassenhaus groups includes two families of finite simple groups: the projective special linear groups 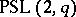, 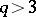(cf. Special linear group), and the Suzuki groups (cf. Suzuki group).

References

[1]	H. Zassenhaus, "Kennzeichnung endlicher linearer Gruppen als Permutationsgruppen" Abh. Math. Sem. Univ. Hamburg , 11 (1935) pp. 17–40
[2]	D. Gorenstein, "Finite groups" , Harper & Row (1968)

References

[a1]	B. Huppert, "Finite groups" , 3 , Springer (1967)