Stopping time

Let 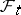, , 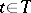be a non-decreasing family of sub-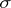-algebras on a measurable space 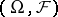, where 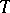is an interval in 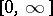or a subset of 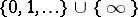. Then a stopping time (relative to this family of subalgebras) is a mapping ( a random variable) 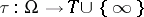such that

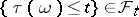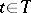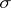for all . Such a random variable is also called an optional random variable. This condition has the interpretation that the (time-valued) random variable has no knowledge of the future, since the -algebra 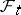embodies "random events up to time t" . Many stopping times arise as "the point of time at which a given random event is observed for the first time" ; for instance, the first time of entry of a stochastic process 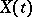into a set 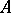(hitting time). In the (translated) Russian literature the phrase Markov moment, or Markov time, is often used for stopping time. Occasionally one also finds the phrase non-anticipating time. Stopping times naturally arise, e.g., in optimal stopping problems, cf., e.g., [a4].

References

[a1]	H. Bauer, "Probability theory and elements of measure theory" , Holt, Rinehart & Winston (1972) pp. 332 (Translated from German)
[a2]	J. Lamperti, "Stochastic processes" , Springer (1977) pp. 210–213
[a3]	K.L. Chung, "Elementary probability theory with stochastic processes" , Springer (1974) pp. 269
[a4]	I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "Controlled stochastic processes" , Springer (1979) (Translated from Russian)
[a5]	M.M. Rao, "Stochastic processes and integration" , Sijthoff & Noordhoff (1979)