Balanced module
From Encyclopedia of Mathematics
A module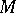 
such that the natural ring homomorphism 
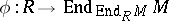, where 
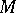is regarded as a right module over 
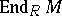, defined by 
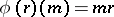for any 
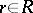and 
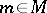, is surjective. A module 
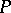over a ring 
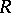is a generator of the category of 
-modules if and only if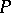 
is balanced as an R-module, projective and finitely generated as an 
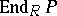-module.
References
| [1] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976) |
How to Cite This Entry:
Balanced module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balanced_module&oldid=42045
Balanced module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balanced_module&oldid=42045
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article