Hilbert-Kamke problem
From Encyclopedia of Mathematics
Revision as of 18:52, 24 March 2012 by Ulf Rehmann (talk | contribs) (moved Hilbert–Kamke problem to Hilbert-Kamke problem: ascii title)
The problem of the compatibility of a system of Diophantine equations of Waring type:
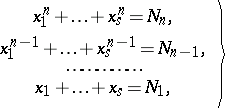 | (*) |
where the  assume integral non-negative values, certain additional restrictions [3] are imposed on the numbers
assume integral non-negative values, certain additional restrictions [3] are imposed on the numbers 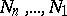 , and
, and  is a sufficiently-large number which depends only on the natural number
is a sufficiently-large number which depends only on the natural number  which is given in advance.
which is given in advance.
The Hilbert–Kamke problem, which was posed in 1900 by D. Hilbert [1], was solved by E. Kamke, who proved that solutions to (*) in fact exist. K.K. Mardzhanishvili in 1937 [3] obtained an asymptotic formula for the number of solutions of this system using the Vinogradov method for estimating trigonometric sums.
References
| [1] | D. Hilbert, "Beweis für die Darstellbarkeit der ganzen Zahlen durch eine feste Anzahl 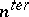 Potenzen (Waringsches Problem)" Math. Ann. , 67 (1909) pp. 281–300 Potenzen (Waringsches Problem)" Math. Ann. , 67 (1909) pp. 281–300 |
| [2] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [3] | K.K. Mardzhanishvili, Izv. Akad. Nauk SSSR Ser. Mat. (1937) pp. 609–631 |
How to Cite This Entry:
Hilbert-Kamke problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Kamke_problem&oldid=42043
Hilbert-Kamke problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert-Kamke_problem&oldid=42043
This article was adapted from an original article by B.M. Bredikhin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article