Weakly infinite-dimensional space

A topological space 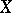such that for any infinite system of pairs of closed subsets 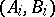of it,

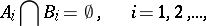there are partitions (cf. Partition) 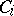(between 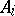and ) such that 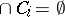. An infinite-dimensional space which is not weakly infinite dimensional is called strongly infinite dimensional. Weakly infinite-dimensional spaces are also called 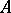-weakly infinite dimensional. If in the above definition it is further required that some finite subfamily of the 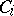's have empty intersection, one obtains the concept of an -weakly infinite-dimensional space.

References

[1]	P.S. Aleksandrov, B.A. Pasynkov, "Introduction to dimension theory" , Moscow (1973) (In Russian)

Comments

In addition to the above, 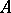-weakly stands for Aleksandrov weakly, and 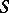-weakly for Smirnov weakly. There is also the obsolete notion of Hurewicz-weakly infinite-dimensional space. Cf. the survey [a1].

To avoid ambiguity in the phrase "infinite-dimensional space" , the space could be required to be metrizable, cf. [a2].

References

[a1]	P.S. Aleksandrov, "Some results in the theory of topological spaces, obtained within the last twenty-five years" Russian Math. Surveys , 15 : 2 (1960) pp. 23–83 Uspekhi Mat. Nauk , 15 : 2 (1960) pp. 25–95
[a2]	J. van Mill, "Infinite-dimensional topology, prerequisites and introduction" , North-Holland (1989) pp. 40
[a3]	R. Engelking, E. Pol, "Countable-dimensional spaces: a survey" Diss. Math. , 216 (1983) pp. 5–41