Bordering of a space

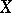in a compactification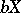

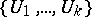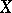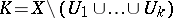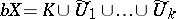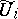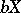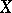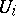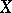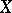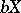A finite family of sets open in such that the set is compact, and , where is the largest open set in the intersection of which with is the set ( is assumed to be completely regular). The concept of a bordering of a space in coincides with the concept of an almost-extendable bordering of a proximity space 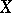(the proximity on 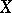is induced by the extension 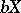), formulated in terms of the proximity: apart from 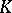being compact, it is necessary that for any neighbourhood 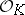, the family 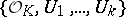is a uniform covering of the space 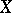. A bordering of a space 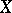in its Stone–Čech compactification is simply called a bordering of 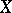. In the language of borderings, a series of theorems has been formulated on the dimensions of the remainder of compactifications of topological and proximity spaces.

References

[1]	Yu.M. Smirnov, "On the dimensions of remainders of compactifications of proximity and topological spaces" Mat. Sb. , 71 : 4 (1966) pp. 554–482 (In Russian)

Comments

A concept related to the bordering of a space is that of a border cover: A collection 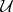of open sets such that 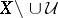is compact. Border covers work in a sense opposite to borderings. In the case of borderings a compactification is given; from certain systems of border covers one can construct compactifications whose remainders can have special properties.