Feathering
of a space
A countable family 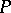 of coverings of a space
of coverings of a space 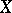 by open sets in an ambient space
by open sets in an ambient space 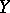 such that
such that
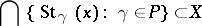 |
for every point 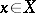 (here
(here 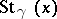 denotes the star of the point
denotes the star of the point  relative to
relative to 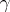 , i.e. the union of all elements of
, i.e. the union of all elements of 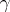 containing the point
containing the point  ).
).
The concept of a feathering forms the basis of the definition of the so-called 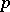 -space (in the sense of A.V. Arkhangel'skii). A space
-space (in the sense of A.V. Arkhangel'skii). A space 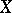 is called a
is called a 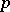 -space if it has a feathering in its Stone–Čech compactification or Wallman compactification. Every complete space (in the sense of Čech) is a
-space if it has a feathering in its Stone–Čech compactification or Wallman compactification. Every complete space (in the sense of Čech) is a  -space. Every
-space. Every 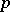 -space has pointwise countable type. In a
-space has pointwise countable type. In a  -space, the addition theorem for weight holds and the net weight coincides with the weight. Paracompact
-space, the addition theorem for weight holds and the net weight coincides with the weight. Paracompact 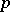 -spaces are perfect pre-images of metric spaces. Paracompact
-spaces are perfect pre-images of metric spaces. Paracompact 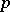 -spaces with a pointwise countable base are metrizable, just as spaces of this type with a
-spaces with a pointwise countable base are metrizable, just as spaces of this type with a 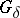 -diagonal are also metrizable. The perfect image and the perfect pre-image of a paracompact
-diagonal are also metrizable. The perfect image and the perfect pre-image of a paracompact 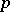 -space are also paracompact
-space are also paracompact 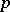 -spaces.
-spaces.
Comments
The word "plumingpluming" is also used instead of feathering. A 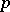 -space is also called a feathered space.
-space is also called a feathered space.
References
| [a1] | "Generalized metric spaces" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set-Theoretic Topology , North-Holland (1984) pp. 423–501 |
Feathering. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Feathering&oldid=41923