Buchstab function
From Encyclopedia of Mathematics
The continuous solution of the system
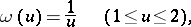 |
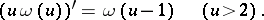 |
This function occurs in number theory as the limit
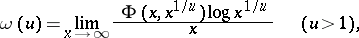 |
where 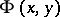 denotes the number of positive integers not exceeding
denotes the number of positive integers not exceeding  that are free of prime factors smaller than
that are free of prime factors smaller than 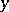 ; see [a1].
; see [a1].
The function 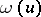 is positive-valued and converges to the constant
is positive-valued and converges to the constant 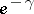 as
as 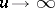 , where
, where 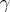 is the Euler constant. The difference
is the Euler constant. The difference 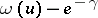 behaves asymptotically like a trigonometric function with period
behaves asymptotically like a trigonometric function with period  and decaying amplitudes of size
and decaying amplitudes of size 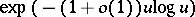 . These and similar results have been exploited in the study of irregularities in the distribution of prime numbers; see [a2], [a3].
. These and similar results have been exploited in the study of irregularities in the distribution of prime numbers; see [a2], [a3].
References
| [a1] | A.A. Bukhstab, "Asymptotic estimates of a general number-theoretic function" Mat. Sb. , 44 (1937) pp. 1239–1246 (In Russian) |
| [a2] | J. Friedlander, A. Granville, A. Hildebrand, H. Maier, "Oscillation theorems for primes in arithmetic progressions and for sifting functions" J. Amer. Math. Soc. , 4 (1991) pp. 25–86 |
| [a3] | H. Maier, "Primes in short intervals" Michigan Math. J. , 32 (1985) pp. 221–225 |
How to Cite This Entry:
Buchstab function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buchstab_function&oldid=41917
Buchstab function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buchstab_function&oldid=41917
This article was adapted from an original article by A. Hildebrand (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article