Buchstab identity

A form of the Sylvester inclusion-and-exclusion principle specialized to sieve theory (cf. also Sieve method). Let 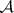be a finite integer sequence and, for any integer 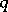, denote by 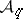the subsequence of elements of 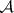that are multiples of 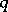. Let be a set of prime numbers (cf. also Prime number), and, for 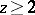, let 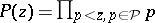. Finally, let

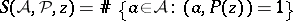denote the "sifting function" associated with 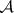and 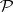. The Bukhstab identity asserts that, for ,

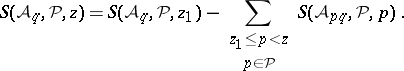(a1)

The identity is useful for deriving a lower-bound sieve estimate from an upper bound sieve estimate (or vice versa) as follows. If the parameter 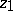is sufficiently small, then the quantity 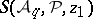on the right-hand side of (a1) usually can be estimated asymptotically. Thus, if an upper bound for each of the terms 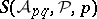on the right-hand side of (a1) is known, then a lower bound for the sifting function on the left-hand side of (a1) can be deduced.

References

[a1]	H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974)