Presentation
of a group
A specification of a group by generators and relations among them.
Comments
Every group can be presented by means of generators and relations. A presentation is finitely generated, respectively finitely related, if the number of generators, respectively relations, is finite. A finite presentation is one with both a finite number of relations and a finite number of generators. A presentation of the symmetric group 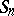 of permutations on
of permutations on  letters is as follows: there are
letters is as follows: there are 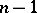 generators
generators 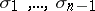 , and the relations are
, and the relations are 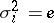 ,
,  if
if 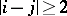 ,
, 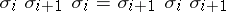 . If the relations
. If the relations 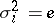 are removed, one obtains a presentation of the braid group (cf. Braid theory).
are removed, one obtains a presentation of the braid group (cf. Braid theory).
If 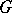 is presented by generators
is presented by generators 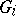 ,
, 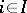 , and relations
, and relations 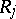 ,
, 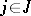 , one writes
, one writes 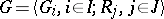 . In that case
. In that case 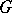 is the quotient group of the free group on the generators
is the quotient group of the free group on the generators 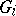 by the normal subgroup generated by the relations
by the normal subgroup generated by the relations 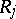 . For details cf. [a1], Sect. 1.2. Given a presentation of a group, there are systematic ways for obtaining presentations of subgroups and quotient groups.
. For details cf. [a1], Sect. 1.2. Given a presentation of a group, there are systematic ways for obtaining presentations of subgroups and quotient groups.
References
| [a1] | W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations of groups in terms of generators and relations" , Wiley (Interscience) (1966) |
| [a2] | H.S.M. Coxeter, W.O.J. Moser, "Generators and relations for discrete groups" , Springer (1965) |
Presentation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Presentation&oldid=41857