Quasi-character
A continuous homomorphism from an Abelian topological group 
into the multiplicative group of complex numbers. In this setting 
is often the multiplicative group 
of some local field 
.
The restriction of a quasi-character 
to any compact subgroup of 
is a character of this subgroup (cf. Character of a group). In particular, if 
is a norm on 
and 
, then 
induces a character 
of the group 
, and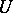 
is, in the non-Archimedean case, the same as the group of units of 
. If 
, then the quasi-character is said to be non-ramified. Any non-ramified quasi-character has the form
 |
In the general case a quasi-character of the group 
has the form 
, where 
is a complex number and 
is a character of 
. The real part of 
is uniquely determined by the quasi-character 
and is called the real part of 
.
In the non-Archimedean case, for each quasi-character 
there is a positive integer 
such that
 |
where 
is the maximal ideal in the ring of integers of 
. The smallest number 
with this property is called the degree of ramification of the quasi-character 
, and the ideal 
is called the conductor of 
.
References
| [1] | S. Lang, "Algebraic numbers" , Addison-Wesley (1964) |
| [2] | I.R. Shafarevich, "The zeta-function" , Moscow (1969) (In Russian) |
Quasi-character. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-character&oldid=41852