Dijkstra algorithm
Dijkstra shortest-path algorithm
Let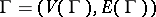 
be a graph with a specified vertex 
and for every edge 
a non-negative cost (length)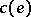 
. The shortest-path problem is to find a shortest path from 
to every other vertex (node)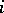 
.
Basically, the Dijkstra algorithm, which solves this problem, is a node-labeling greedy algorithm. It proceeds by constructing, one node at a time, a subtree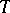 
rooted at 
(an 
-arborescence). If 
is connected,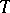 
will be a spanning subtree (at the end).
Initially,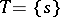 
. At any further step one knows the shortest distance 
and corresponding path from 
to any vertex 
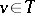. This is the label of 
. Of course,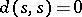 
.
Now, look through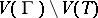 
for a vertex 
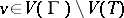and a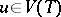 
for which 
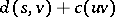is minimal, and add 
and the edge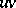 
to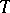 
.
The algorithm stops as soon as 
spans the connected component of 
in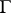 
. The shortest path from 
to any 
in the connected component of 
in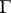 
is given by the unique path in 
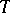from 
to 
; the length is 
.
A very rough implementation of Dijkstra's algorithm takes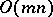 
steps, where 
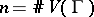, the cardinality of the vertex set of 
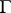, and 
, the cardinality of the set of edges of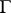 
. It can be done much more efficiently, [a3].
The algorithm can be easily adapted to directed edge-weighted graphs and networks. As of 2001, there is no efficient algorithm for finding longest paths in loop-free (directed) graphs.
References
| [a1] | A. Frank, "Connectivity and network flows" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovász (ed.) , Handbook of Combinatorics , Elsevier (1995) pp. 111–178 |
| [a2] | "Encyclopedia of Operations Research and Management Science" S.I. Gass (ed.) C.M. Harris (ed.) , Kluwer Acad. Publ. (1996) pp. 166–167 |
| [a3] | L. Lovász, D.B. Shmoys, E. Tardos, "Combinatorics in computer science" R.L. Graham (ed.) M. Grötschel (ed.) L. Lovász (ed.) , Handbook of Combinatorics , Elsevier (1995) pp. 2003–2038 |
Dijkstra algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dijkstra_algorithm&oldid=41834