Split sequence
From Encyclopedia of Mathematics
split exact sequence, split short exact sequence
 | (*) |
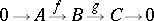in an Abelian category which is isomorphic to the direct sum sequence,
 |
by an isomorphism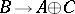 
which induces the identity on 
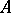and on 
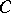. Sufficient conditions for an exact sequence (*) to be split are the existence of a right inverse 
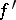for 
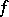, or of a left inverse 
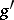for 
. The class of split exact sequences is the zero of the group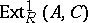 
(see Baer multiplication). In a category of vector spaces (that is, of modules over a fixed field) every exact sequence splits.
For relative homological algebra, the typical situation is to consider exact sequences in one category which split in another.
Comments
References
| [a1] | S. MacLane, "Homology" , Springer (1963) pp. 16, 260 |
How to Cite This Entry:
Split sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Split_sequence&oldid=41781
Split sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Split_sequence&oldid=41781
This article was adapted from an original article by V.E. Govorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article