Conditional mathematical expectation
conditional expectation, of a random variable
A function of an elementary event that characterizes the random variable with respect to a certain 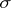 -algebra. Let
-algebra. Let 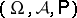 be a probability space, let
be a probability space, let  be a real-valued random variable with finite expectation defined on this space and let
be a real-valued random variable with finite expectation defined on this space and let 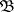 be a
be a 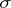 -algebra,
-algebra, 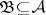 . The conditional expectation of
. The conditional expectation of  with respect to
with respect to 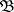 is understood to be a random variable
is understood to be a random variable 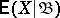 , measurable with respect to
, measurable with respect to 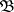 and such that
and such that
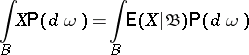 | (*) |
for each 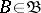 . If the expectation of
. If the expectation of 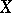 is infinite (but defined), i.e. only one of the numbers
is infinite (but defined), i.e. only one of the numbers 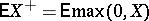 and
and 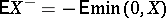 is finite, then the definition of the conditional expectation by means of (*) still makes sense but
is finite, then the definition of the conditional expectation by means of (*) still makes sense but 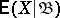 may assume infinite values.
may assume infinite values.
The conditional expectation is uniquely defined up to equivalence. In contrast to the mathematical expectation, which is a number, the conditional expectation represents a function (a random variable).
The properties of the conditional expectation are similar to those of the expectation:
1) 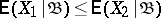 if, almost certainly,
if, almost certainly, 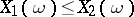 ;
;
2) 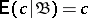 for every real
for every real  ;
;
3) 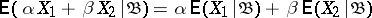 for arbitrary real
for arbitrary real 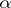 and
and 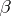 ;
;
4) 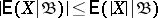 ;
;
5) 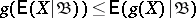 for every convex function
for every convex function 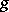 . Furthermore, the following properties specific to the conditional expectation hold:
. Furthermore, the following properties specific to the conditional expectation hold:
6) If 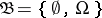 is the trivial
is the trivial 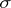 -algebra, then
-algebra, then 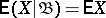 ;
;
7) 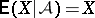 ;
;
8) 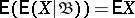 ;
;
9) if 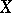 is independent of
is independent of 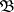 , then
, then 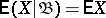 ;
;
10) if 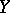 is measurable with respect to
is measurable with respect to 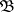 , then
, then 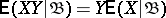 .
.
There is a theorem on convergence under the integral sign of conditional mathematical expectation: If 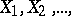 is a sequence of random variables,
is a sequence of random variables, 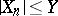 ,
, 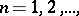
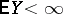 and
and 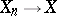 almost certainly, then, almost certainly,
almost certainly, then, almost certainly, 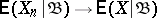 .
.
The conditional expectation of a random variable 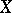 with respect to a random variable
with respect to a random variable 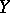 is defined as the conditional expectation of
is defined as the conditional expectation of 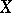 relative to the
relative to the 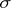 -algebra generated by
-algebra generated by 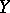 .
.
A particular case of the conditional expectation is the conditional probability.
References
| [1] | A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from Russian) |
| [2] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1969) (Translated from Russian) |
| [3] | J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970) |
| [4] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) |
Comments
Almost-certain convergence is also called almost-sure convergence in the West.
References
| [a1] | R.B. Ash, "Real analysis and probability" , Acad. Press (1972) |
| [a2] | J. Neveu, "Discrete-parameter martingales" , North-Holland (1975) (Translated from French) |
Conditional mathematical expectation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conditional_mathematical_expectation&oldid=41628