Formal systems, equivalence of
From Encyclopedia of Mathematics
Two formal systems (cf. Formal system) are called equivalent if the sets of expressions that are deducible in these systems are identical. More precisely, two formal systems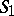 
and 
are equivalent if and only if the following conditions are satisfied: 1) every axiom of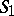 
is deducible in 
; 2) every axiom of 
is deducible in 
; 3) if an expression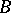 
follows immediately from expressions 
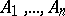by virtue of a derivation rule of 
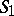, and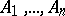 
are deducible in 
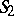, then 
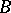is also deducible in 
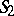; and 4) the same as 3) with 
and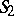 
interchanged.
How to Cite This Entry:
Formal systems, equivalence of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formal_systems,_equivalence_of&oldid=41452
Formal systems, equivalence of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formal_systems,_equivalence_of&oldid=41452
This article was adapted from an original article by V.E. Plisko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article