Universal enveloping algebra

of a Lie algebra 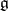over a commutative ring 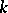with a unit element

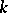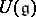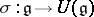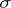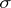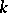The associative -algebra with a unit element, together with a mapping for which the following properties hold: 1) is a homomorphism of Lie algebras, i.e. is -linear and 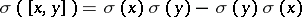, ; 2) for every associative 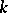-algebra 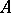with a unit element and every 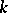-algebra mapping 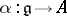such that 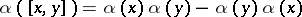, , 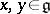there exists a unique homomorphism of associative algebras 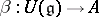, mapping the unit to the unit, such that 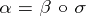. The universal enveloping algebra is unique up to an isomorphism and always exists: If 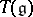is the tensor algebra of the 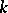-module 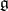, 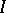is the two-sided ideal generated by all elements of the form 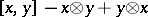, , 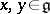and 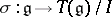is the canonical mapping, then 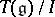is the universal enveloping algebra of .

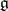If 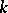is Noetherian and the module 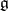has finite order, then the algebra 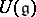is left and right Noetherian. If 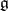is a free module over an integral domain 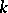, then 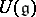has no zero divisors. For any finite-dimensional Lie algebra 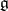over a field 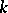the algebra 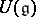satisfies the Ore condition (cf. Imbedding of semi-groups) and so has a skew-field of fractions.

If 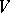is any 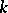-module, then every homomorphism of Lie algebras 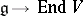extends to a homomorphism of associative algebras 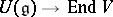. This establishes an isomorphism of the category of 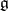-modules and the category of left 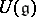-modules, whose existence forms the basis for the application of universal enveloping algebras in the theory of representations of Lie algebras (cf. [3], [4]).

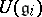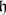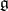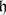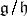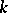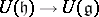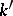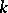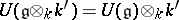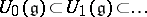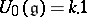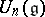The universal enveloping algebra of the direct product of Lie algebras is the tensor product of the algebras . If is a subalgebra of , where and are free -modules, then the canonical homomorphism is an imbedding. If is an extension of the field , then . A universal enveloping algebra has a canonical filtration , where and for 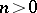is the 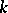-submodule of 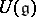generated by the products 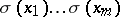, , 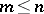for all 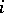. The graded algebra 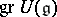associated to this filtration is commutative and is generated by the image under the natural homomorphism ; this mapping defines a homomorphism 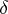of the symmetric algebra 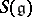of the 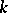-module 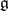onto 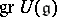. By the Poincaré–Birkhoff–Witt theorem, 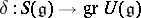is an algebra isomorphism if 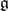is a free 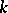-module. The following is an equivalent formulation: If 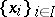is a basis of the 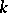-module 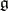, where 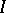is a totally ordered set, then the family of monomials 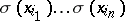, , 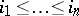, 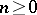forms a basis of the 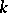-module 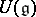(in particular, 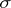is injective).

Let 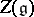be the centre of 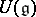. Then for any finite-dimensional Lie algebra 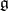over a field of characteristic zero, 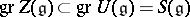consists of the subalgebra of 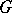-invariant elements in 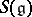. If 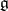is semi-simple, then 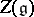is the algebra of polynomials in variables.

One of the important directions of research in universal enveloping algebra is the study of primitive ideals (cf. Primitive ideal; [3]).

References

[1]	N. Bourbaki, "Lie groups and Lie algebras" , Elements of mathematics , Hermann (1975) pp. Chapts. 1–3 (Translated from French)
[2]	N. Bourbaki, "Groupes et algèbres de Lie" , Hermann (1975) pp. Chapts. VII-VIII
[3]	J. Dixmier, "Enveloping algebras" , North-Holland (1977) (Translated from French)
[4]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[5]	I.M. Gel'fand, "The centre of an infinitesimal group ring" Mat. Sb. , 26 (1950) pp. 103–112 (In Russian)
[6]	J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French)

References

[a1]	J.C. Jantzen, "Einhüllende Algebren halbeinfacher Lie-Algebren" , Springer (1983)