Loss function

In a problem of statistical decision making, a non-negative function indicating the loss (cost) to an experimenter given a particular state of the world and a particular decision. Let be a random variable taking values in a sample space , , and let 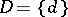be the space of all possible decisions that can be taken on the basis of an observed . In the theory of statistical decision functions, any non-negative function defined on is called a loss function. The value of a loss function 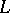at an arbitrary point is interpreted as the cost incurred by taking a decision 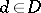, when the true parameter is , .

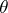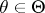References

[1]	A. Wald, "Statistical decision functions" , Wiley (1950)
[2]	E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986)

References

[a1]	J.O. Berger, "Statistical decision theory and Bayesian analysis" , Springer (1985)