Equilibrium relation
A relation expressing the connection between the growth of a function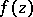 
that is meromorphic for 
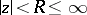, and its value distribution (see Value-distribution theory). Each meromorphic function 
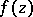has the following equilibrium property: The sum of its counting function 
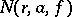, which characterizes the density of the distribution of 
-points of 
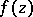, and the proximity function 
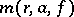, which characterizes the average rate of approximation of 
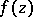to the given number 
, is invariant for different values of 
. The equilibrium relation becomes more effective when using the spherical metric.
Let
 |
denote the spherical distance between two numbers 
and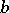 
, and, for each complex number 
, let
 |
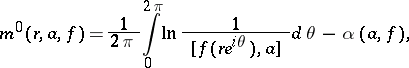where
 |
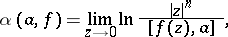and let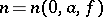 
denote the multiplicity of 
-points of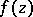 
for 
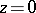. As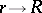 
the function 
differs from the Nevanlinna proximity function 
by a bounded term. Therefore, on a circle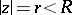 
, the function 
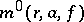, as before, characterizes the average rate of approximation of 
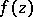to 
. The following result holds. For each value 
, 
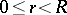, for any complex number 
in the extended complex plane and for an arbitrary function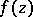 
that is meromorphic in 
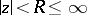, the equality (the equilibrium relation)
 |
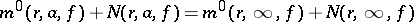holds, where
 |
and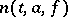 
denotes the number of 
-points of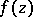 
in the disc 
.
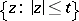After the foundational work of R. Nevanlinna [1], the equilibrium relation was carried over to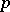 
-dimensional entire curves (see [3]) and to holomorphic mappings (see [4], [5]).
References
| [1] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [2] | H. Wittich, "Neueste Ergebnisse über eindeutige analytische Funktionen" , Springer (1955) |
| [3] | H. Weyl, "Meromorphic functions and analytic curves" , Princeton Univ. Press (1943) |
| [4] | B.V. Shabat, "Introduction of complex analysis" , 2 , Moscow (1976) (In Russian) |
| [5] | P. Griffiths, J. King, "Nevanlinna theory and holomorphic mappings between algebraic varieties" Acta Math. , 130 (1973) pp. 145–220 |
Comments
An 
-point of a function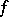 
is a point 
such that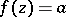 
.
The equilibrium relation is often referred to as the "Ahlfors–Shimizu version of Nevanlinna's first main theoremAhlfors–Shimizu version of Nevanlinna's first main theorem" .
See also Nevanlinna theorems and Value-distribution theory for the notions of counting function and proximity function.
References
| [a1] | P.A. Griffiths, "Entire holomorphic mappings in one and several complex variables" , Annals Math. Studies , 85 , Princeton Univ. Press (1976) |
Equilibrium relation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equilibrium_relation&oldid=40766