Matrix differential equation

An equation in which the unknown is a matrix of functions appearing in the equation together with its derivative.

Consider a linear matrix differential equation of the form

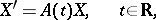(1)

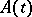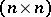where is an -dimensional matrix function with locally Lebesgue-integrable entries, and let 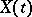be an absolutely-continuous solution of equation (1) satisfying the condition 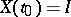, where 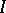is the identity matrix. Then the vector function 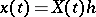, , 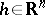is a solution of the linear system

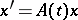(2)

satisfying the condition 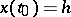. Conversely, if 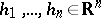and 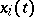is a solution of the system (2) satisfying the condition 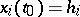, , 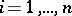then the matrix 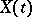with as columns the solutions 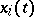is a solution of the matrix differential equation (1). If, in addition, the vectors 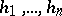are linearly independent, then 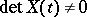for all .

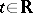Equation (1) is a particular case of the following matrix differential equation (arising in the theory of stability)

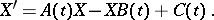(3)

The solution of (3) with initial condition 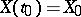is given by the formula

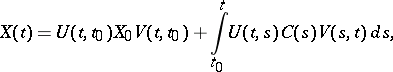where 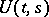is the solution of (1) with the condition 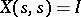, and 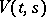is the solution of the matrix differential equation 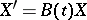with the condition .

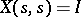In various applied problems (theories of stabilization, optimal control, filtration of control system, and others) an important role is played by the so-called matrix Riccati differential equation

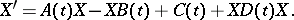Thus, if the matrix Riccati equation

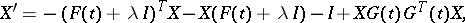where 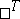stands for transposition, has for 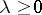a bounded solution 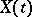on the line 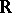, and if for 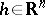all , all 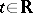, and some 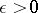, the inequality 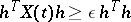holds, then every solution of the controllable system

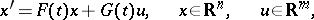closed by the feedback law 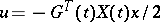, satisfies the inequality

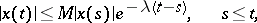where is the Euclidean norm and 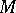does not depend on .

References

[1]	I.A. Lappo-Danilevsky, "Mémoire sur la théorie des systèmes des équations différentielles linéaires" , Chelsea, reprint (1953)
[2]	Yu.L. Daletskii, M.G. Krein, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian)
[3]	F.V. Atkinson, "Discrete and continuous boundary problems" , Acad. Press (1964)
[4]	W.T. Reid, "Riccati differential equations" , Acad. Press (1972)
[5]	M.Kh. Zakhar-Itkin, "The matrix Riccati differential equation and the semi-group of linear fractional transformations" Russian Math. Surveys , 28 : 3 (1973) pp. 89–131 Uspekhi Mat. Nauk , 28 : 3 (1973) pp. 83–120

References

[a1]	J.K. Hale, "Ordinary differential equations" , Wiley (1969)