Jacobi equation

A first-order ordinary differential equation

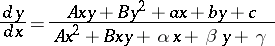or, in a more symmetric form,

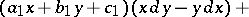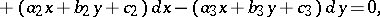where all the coefficients are constant numbers. This equation, which is a special case of the Darboux equation, was first studied by C.G.J. Jacobi [1]. The Jacobi equation is always integrable in closed form by using the following algorithm. First one finds by direct substitution at least one particular linear solution

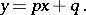Then one makes the changes of variables

to obtain an equation that is reducible to a homogeneous equation.

References

[1]	C.G.J. Jacobi, "De integratione aequationis differentialis 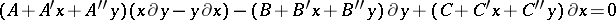" J. Reine Angew. Math. , 24 (1842) pp. 1–4
[2]	W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)
[3]	E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1947)

References

[a1]	E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956)