Grothendieck functor

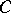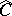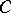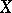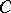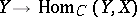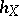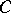An imbedding functor (cf. Imbedding of categories) from a category into the category of contravariant functors defined on and taking values in the category of sets (Ens). Let be an object in a category ; the mapping defines a contravariant functor from into the category of sets. For any object 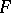of 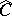there exists a natural bijection (Yoneda's lemma). Hence, in particular

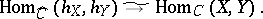Accordingly, the mapping 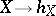defines a full imbedding 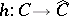, which is known as the Grothendieck functor. Using the Grothendieck functor it is possible to define algebraic structures on objects of a category (cf. Group object; Group scheme).

References

[1]	I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968)
[2]	A. Grothendieck, "Technique de descente et théorèmes d'existence en géométrie algébrique, II" Sem. Bourbaki , Exp. 195 (1960)

Comments

In the English literature, the Grothendieck functor is commonly called the Yoneda embedding or the Yoneda–Grothendieck embedding.

References

[a1]	S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7
[a2]	N. Yoneda, "On the homology theory of modules" J. Fac. Sci. Tokyo. Sec. I , 7 (1954) pp. 193–227