Duhamel integral

A representation of the solution of the Cauchy problem (or of a mixed problem) for an inhomogeneous linear partial differential equation with homogeneous boundary conditions by means of the solution of the corresponding problem for the homogeneous equation. Consider the equation

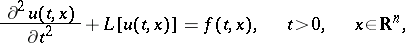(1)

where 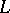is a linear differential operator with coefficients independent of 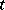, containing derivatives in 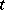of order not exceeding 1. The Cauchy problem for (1) is posed with the initial conditions:

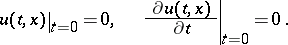(2)

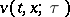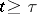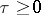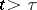Let the sufficiently smooth function , , , , for , be a solution of the homogeneous equation

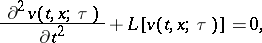and let it satisfy, for 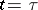, the initial conditions

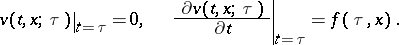Then the solution of the Cauchy problem (1), (2) is given by the Duhamel integral

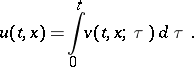This theorem, known as Duhamel's principle, is an analogue of the method of variation of constants.

A similar construction can be used for the Cauchy problem with a homogeneous initial condition for the equation

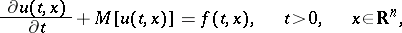where 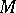is a linear differential operator with coefficients independent of 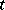, containing derivatives with respect to the variable only.

The solution of the Cauchy problem with homogeneous initial conditions for the inhomogeneous heat equation is expressed by the Duhamel integral

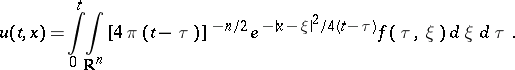For the wave equation if 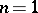one has:

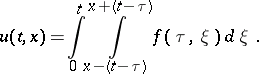The integral is named after J. Duhamel.

References

[1]	A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian)
[2]	F. John, "Planar waves and spherical means as applied to partial differential equations" , Interscience (1955)

References

[a1]	H.S. Carslaw, J.C. Jaeger, "Conduction of heat in solids" , Clarendon Press (1959)