Analytic vector
in the space 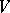 of a representation
of a representation 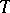 of a Lie group
of a Lie group 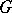
A vector 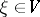 for which the mapping
for which the mapping 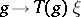 is a real-analytic vector function on
is a real-analytic vector function on 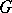 with values in
with values in 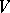 (cf. Representation theory). If
(cf. Representation theory). If 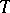 is a weakly-continuous representation of a Lie group
is a weakly-continuous representation of a Lie group 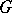 in a Banach space
in a Banach space 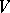 , then the set
, then the set 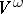 of analytic vectors is dense in
of analytic vectors is dense in  [1], [2], [3]. This theorem has been generalized to a wide class of representations in locally convex spaces [5]. It has been proved [6] that a representation of a connected Lie group
[1], [2], [3]. This theorem has been generalized to a wide class of representations in locally convex spaces [5]. It has been proved [6] that a representation of a connected Lie group 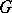 in a Banach space
in a Banach space 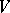 is uniquely determined by the corresponding representation of the Lie algebra of the Lie group
is uniquely determined by the corresponding representation of the Lie algebra of the Lie group 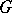 in the space
in the space 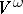 .
.
An analytic vector for an unbounded operator  on a Banach space
on a Banach space 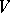 , defined on a domain
, defined on a domain 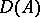 , is defined as a vector
, is defined as a vector
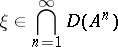 |
for which the series
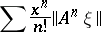 |
has a positive radius of convergence. This notion, which was introduced in [2], is a special case of the general concept of an analytic vector; here the set of points on the real line with the addition operation plays the role of the Lie group 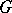 . It was found useful in the theory of operators on Banach spaces and in the theory of elliptic differential operators.
. It was found useful in the theory of operators on Banach spaces and in the theory of elliptic differential operators.
References
| [1] | P. Cartier, J. Dixmier, "Vecteurs analytiques dans les répresentations de groupes de Lie" Amer. J. Math. , 80 (1958) pp. 131–145 |
| [2] | E. Nelson, "Analytical vectors" Ann. of Math. , 70 (1969) pp. 572–615 |
| [3] | L. Gårding, "Vecteurs analytiques dans les répresentations des groups" Bull. Soc. Math. France , 88 (1960) pp. 73–93 |
| [4] | P. Cartier, "Vecteurs analytiques" , Sem. Bourbaki 1958/1959 , 181 (1959) pp. 12–27 |
| [5] | R.T. Moore, "Measurable, continuous and smooth vectors for semigroup and group representations" Mem. Amer. Math. Soc. , 78 (1968) |
| [6] | Harish-Chandra, "Representations of a semisimple Lie group on a Banach space I" Trans. Amer. Math. Soc. , 75 (1953) pp. 185–243 |
Comments
Integrability to the corresponding (simply-connected and connected) Lie group 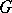 of a representation of a Lie algebra
of a representation of a Lie algebra 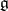 in a Hilbert space follows from the existence of a dense set of analytic vectors for the "Laplacian"
in a Hilbert space follows from the existence of a dense set of analytic vectors for the "Laplacian" 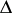 , the sum of the squares of skew-symmetric representatives with a common dense invariant domain
, the sum of the squares of skew-symmetric representatives with a common dense invariant domain 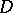 , of linear generators of
, of linear generators of 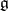 (Nelson's criterion, [2]). More practical criteria were developed later, e.g. the existence of common analytic vectors for Lie generators (the
(Nelson's criterion, [2]). More practical criteria were developed later, e.g. the existence of common analytic vectors for Lie generators (the 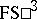 criterion, [a2], [a3], [a4]), as well as similar results in more general spaces and a study of separate versus joint analyticity.
criterion, [a2], [a3], [a4]), as well as similar results in more general spaces and a study of separate versus joint analyticity.
References
| [a1] | G. Warner, "Harmonic analysis on semi-simple Lie groups" , 1 , Springer (1972) |
| [a2] | M. Flato, D. Sternheimer, "Deformations of Poisson brackets, separate and joint analyticity in group representations, nonlinear group representations and physical applications" J.A. Wolf (ed.) M. Cahen (ed.) M. De Wilde (ed.) , Harmonic Analysis and Representations of Semisimple Lie Groups , Reidel (1980) pp. 385–448 |
| [a3] | J. Simon, "On the integrability of representations of finite dimensional real Lie algebras" Commun. Math. Phys. , 28 (1972) pp. 39–46 |
| [a4] | M. Flato, J. Simon, H. Snellman, D. Sternheimer, "Simple facts about analytic vectors and integrability" Ann. Scient. Ec. Norm. Sup. Ser. 4 , 5 (1972) pp. 423–434 |
Analytic vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_vector&oldid=40208