Inessential mapping

homotopically-trivial mapping

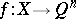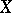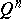A continuous mapping of a topological space into the -dimensional ball such that there is a continuous mapping 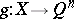that coincides with 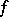on the inverse image 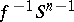of the boundary 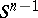of 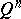and takes 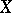into 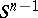(that is, 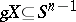). When 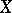is a normal Hausdorff space, then 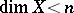if and only if every continuous mapping 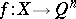, 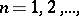is inessential (Aleksandrov's theorem).

A continuous mapping of a topological space into the -dimensional sphere is called inessential if it is homotopic to the constant mapping.

Comments

The term "homotopically-trivial mapping" is not used in the context . See [a1], [a2] and [a3].

Generally, a mapping which is homotopic to a constant mapping is called nullhomotopic or homotopically trivial; in [a3] they are called inessential. See also Essential mapping.

References

[a1]	P.S. Aleksandrov, "Topologie" , 1 , Springer (1974)
[a2]	R. Engelking, "Dimension theory" , PWN (1977)
[a3]	W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948)