Bessel system
From Encyclopedia of Mathematics
A concept in the theory of orthogonal systems. Let 
and 
be two complete systems of functions in 
(i.e. measurable functions that are square-integrable on the segment 
), forming a biorthogonal system of functions. The system 
is said to be a Bessel system if, for any function 
, the series
 |
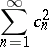is convergent; here, 
are the coefficients of the expansion
 |
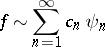of the function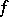 
with respect to the system 
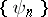. For a system 
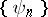to be a Bessel system it is necessary and sufficient that it be possible to define a bounded linear operator 
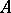on the space 
such that the system 
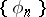defined by the equation 
(
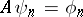) is a complete orthonormal system. If the system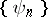 
is a Bessel system, there exists a constant 
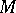such that for any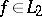 
 |
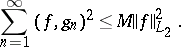References
| [1] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
How to Cite This Entry:
Bessel system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_system&oldid=40179
Bessel system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_system&oldid=40179
This article was adapted from an original article by P.I. Lizorkin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article