World line
A line in space-time which is the space-time trajectory of a material point. Introduce a local coordinate system  , in some domain of space-time, and let the point
, in some domain of space-time, and let the point 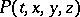 lie on a world line
lie on a world line 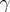 .
. 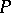 is called a world point; it describes the event that at time
is called a world point; it describes the event that at time 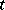 the material point
the material point 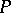 has space coordinates
has space coordinates 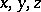 . The concept of an event, and the related concepts of a world point and a world line are among the basic notions of relativity theory, adding to the concept of a material point borrowed from classical mechanics. Usually one considers smooth (or piecewise-smooth) world lines. The world line of a material point with positive rest mass is a time-like curve. The world line of a material point with zero rest mass (such as a non-quantum model of a photon and other elementary particles of mass zero) is an isotropic line. An arbitrary point of space-time is considered as a world point, that is, a (potential) event, and each time-like or isotropic line as the (possible) world line of some material point. The world line of a material point not under the influence of non-gravitational fields is, according to the geodesic hypothesis, a space-time geodesic. The unit tangent vector
. The concept of an event, and the related concepts of a world point and a world line are among the basic notions of relativity theory, adding to the concept of a material point borrowed from classical mechanics. Usually one considers smooth (or piecewise-smooth) world lines. The world line of a material point with positive rest mass is a time-like curve. The world line of a material point with zero rest mass (such as a non-quantum model of a photon and other elementary particles of mass zero) is an isotropic line. An arbitrary point of space-time is considered as a world point, that is, a (potential) event, and each time-like or isotropic line as the (possible) world line of some material point. The world line of a material point not under the influence of non-gravitational fields is, according to the geodesic hypothesis, a space-time geodesic. The unit tangent vector 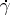 to a world line
to a world line 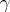 is a four-dimensional velocity vector; in local coordinates it has the form
is a four-dimensional velocity vector; in local coordinates it has the form
 |
where
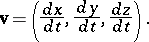 |
See also Minkowski space.
Comments
References
| [a1] | E.F. Taylor, J.A. Wheeler, "Space-time physics" , Freeman (1963) |
| [a2] | A.S. Eddington, "The mathematical theory of relativity" , Cambridge Univ. Press (1960) |
| [a3] | P.G. Bergmann, "Introduction to the theory of relativity" , Dover, reprint (1976) |
| [a4] | D.F. Lawden, "Tensor calculus and relativity" , Methuen (1962) |
World line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=World_line&oldid=40155