Flatness theorem
From Encyclopedia of Mathematics
(in the geometry of numbers)
Let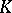 
be a closed bounded convex set in 
of non-zero volume. If the width of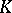 
is at least 
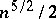, then 
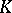contains an element of the integer lattice 
.
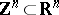Here, the width of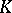 
(with respect to 
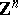) is the minimum width of 
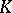along any non-zero integer vector. The width of 
along a vector 
in 
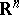is
 |
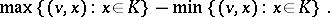The width of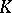 
with respect to 
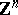is greater or equal than the geometric width of 
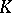, which is the minimum width of 
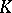along all unit-length vectors.
If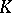 
is a rational polyhedron, i.e. is defined by a system of linear inequalities with rational coefficients, then the "non-zero volume condition" in the flatness theorem can be dispensed with. The flatness theorem finds application in, e.g., the Frobenius problem.
References
| [a1] | J. Hastad, "Dual vectors and lower bounds for the nearest lattice point problem" Combinatorica , 8 (1988) pp. 75–81 |
| [a2] | J. Lagarias, H.W. Lenstra, C.P. Schnorr, "Korkine–Zolotarev bases and successive minima of a lattice and its reciprocal lattice" Combinatorica , 10 (1990) pp. 333–348 |
How to Cite This Entry:
Flatness theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flatness_theorem&oldid=40024
Flatness theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flatness_theorem&oldid=40024
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article