Holley inequality
From Encyclopedia of Mathematics
An inequality for a finite distributive lattice  , saying that if
, saying that if 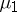 and
and 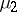 map
map 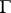 into
into 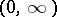 and satisfy
and satisfy 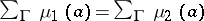 and
and
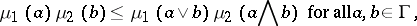 |
then
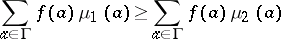 |
for every 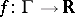 that is non-decreasing in the sense that
that is non-decreasing in the sense that 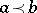 implies
implies 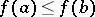 . It is due to R. Holley [a4] and was motivated by the related FKG inequality [a3]. It is an easy corollary [a2] of the more powerful Ahlswede–Daykin inequality [a1].
. It is due to R. Holley [a4] and was motivated by the related FKG inequality [a3]. It is an easy corollary [a2] of the more powerful Ahlswede–Daykin inequality [a1].
See also Correlation inequalities; Fishburn–Shepp inequality.
References
| [a1] | R. Ahlswede, D.E. Daykin, "An inequality for the weights of two families, their unions and intersections" Z. Wahrscheinlichkeitsth. verw. Gebiete , 43 (1978) pp. 183–185 |
| [a2] | P.C. Fishburn, "Correlation in partially ordered sets" Discrete Appl. Math. , 39 (1992) pp. 173–191 |
| [a3] | C.M. Fortuin, P.N. Kasteleyn, J. Ginibre, "Correlation inequalities for some partially ordered sets" Comm. Math. Phys. , 22 (1971) pp. 89–103 |
| [a4] | R. Holley, "Remarks on the FKG inequalities" Comm. Math. Phys. , 36 (1974) pp. 227–231 |
How to Cite This Entry:
Holley inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holley_inequality&oldid=40021
Holley inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holley_inequality&oldid=40021
This article was adapted from an original article by P.C. Fishburn (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article