Normal section

of a smooth surface 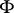at a point 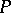in a direction

The section of 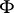by the plane passing through the normal to the surface (cf. Normal space (to a surface)) at 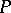and through the direction in the tangent plane to 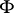at 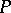. The task of studying the local structure of a surface can be reduced to the same task for the family of curves formed by the normal sections of the surface at a given point in various directions (see Curvature; Normal curvature). The method of studying the local structure by means of normal sections can be generalized to surfaces of arbitrary dimension and arbitrary codimension.

References

[a1]	W. Klingenberg, "A course in differential geometry" , Springer (1978) (Translated from German)
[a2]	B.-Y. Chen, "Geometry of submanifolds" , M. Dekker (1973)