Kakutani theorem

Let 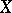be a non-empty compact subset of 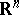, let 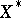be the set of its subsets and let 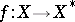be an upper semi-continuous mapping such that for each 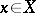the set 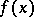is non-empty, closed and convex; then 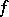has a fixed point (i.e. there is a point 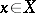such that 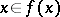). S. Kakutani showed [1] that from his theorem the minimax principle for finite games does follow.

References

[1]	S. Kakutani, "A generalization of Brouwer's fixed point theorem" Duke Math. J. , 8 : 3 (1941) pp. 457–459
[2]	Ky Fan, "Fixed point and minimax theorems in locally convex topological linear spaces" Proc. Nat. Acad. Sci. USA , 38 (1952) pp. 121–126
[3]	H. Nikaido, "Convex structures and economic theory" , Acad. Press (1968)

References

[a1]	J. Dugundji, A. Granas, "Fixed point theory" , 1 , PWN (1982)