Galilean space

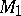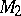The space-time of classical mechanics according to Galilei–Newton, in which the distance between two events taking place at the points and at the moments of time 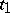and 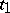is taken to be the time interval 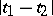, while if these events take place at the same time, it is considered to be the distance between the points and 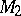. For an -dimensional Galilean space, the distance is defined as follows:

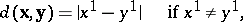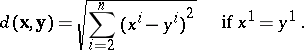A Galilean space is a semi-pseudo-Euclidean space of nullity one; it may be considered as the limit case of a pseudo-Euclidean space in which the isotropic cone degenerates to a plane. This limit transition corresponds to the limit transition from the special theory of relativity to classical mechanics.

References

[1]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)
[2]	R. Penrose, "Structure of space-time" C.M. DeWitt (ed.) J.A. Wheeler (ed.) , Batelle Rencontres 1967 Lectures in Math. Physics , Benjamin (1968) pp. 121–235 (Chapt. VII)