Nash theorem (in game theory)
From Encyclopedia of Mathematics
A theorem on the existence of equilibrium points in a mixed extension of a finite non-cooperative game
 |
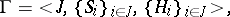where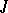 
and 
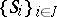are the finite sets of players and their strategies, respectively, and 
: 
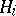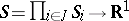is the pay-off function of player 
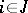(see also Games, theory of). It was established by J. Nash in [1]. Let 
, 
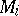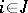, be the set of all probability measures on 
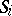. Nash' theorem asserts that there is a measure 
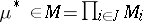for which
 |
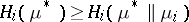for all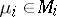 
, 
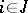, where 
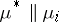denotes the measure from 
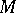that results from replacing the 
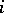-th component of the vector 
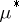by 
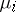, and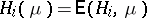 
. The known proofs of Nash' theorem rely on a fixed-point theorem.
References
| [1] | J. Nash, "Non-cooperative games" Ann. of Math. , 54 (1951) pp. 286–295 |
| [2] | N.N. Vorob'ev, "Foundations of game theory. Non-cooperative games" , Moscow (1984) (In Russian) |
| [3] | N.N. Vorob'ev, "Game theory. Lectures for economists and system scientists" , Springer (1977) (Translated from Russian) |
How to Cite This Entry:
Nash theorem (in game theory). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nash_theorem_(in_game_theory)&oldid=40004
Nash theorem (in game theory). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nash_theorem_(in_game_theory)&oldid=40004
This article was adapted from an original article by E.B. Yanovskaya (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article